Spectral Laplacian solver
fun with Fourier-Bessel series and quantum vortices! :>
This project develops a fast and accurate Fourier-Bessel based spectral Laplacian solver in 2D polar coordinates using discrete Hankel transform. We use it to study quantum vortices in Bose-Einstein condensates and some other physical equations associated with Laplacian operator!
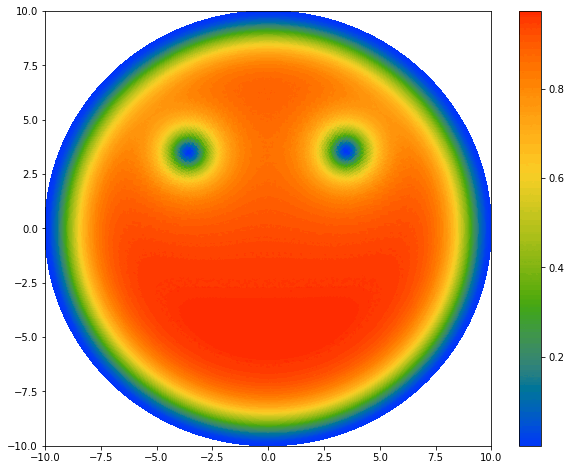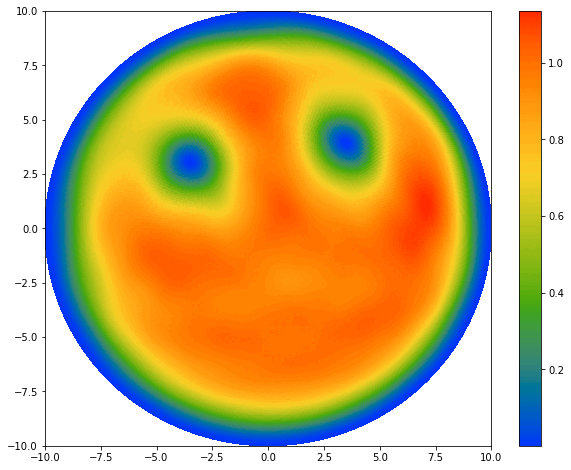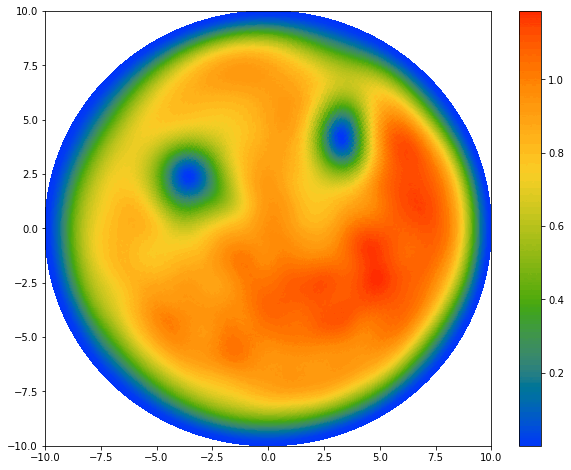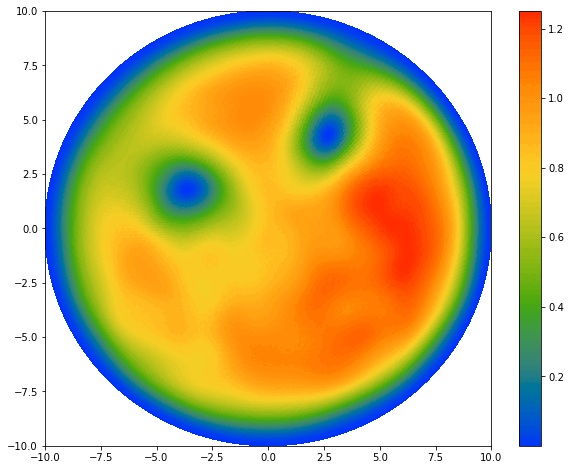
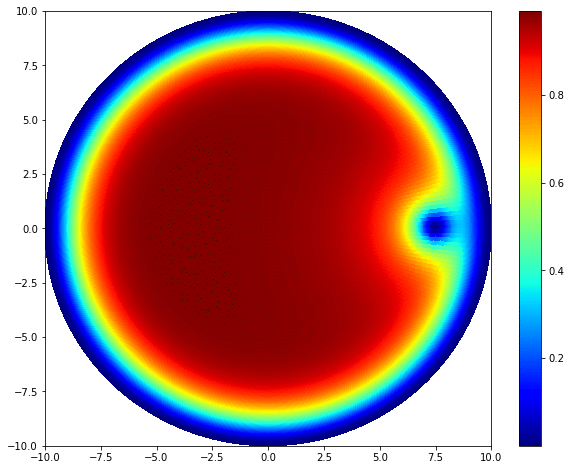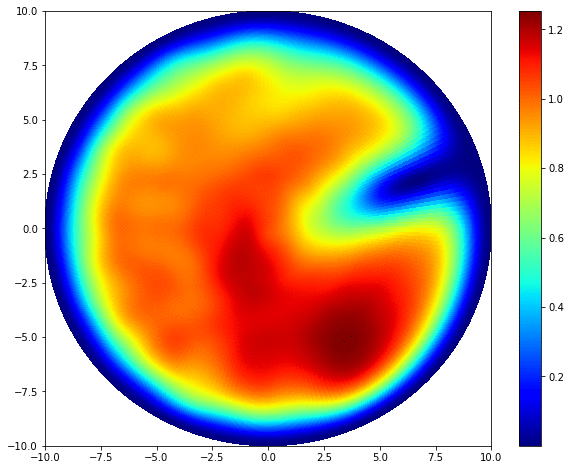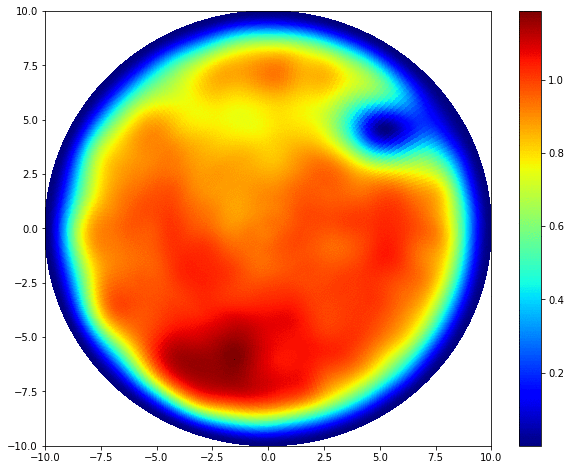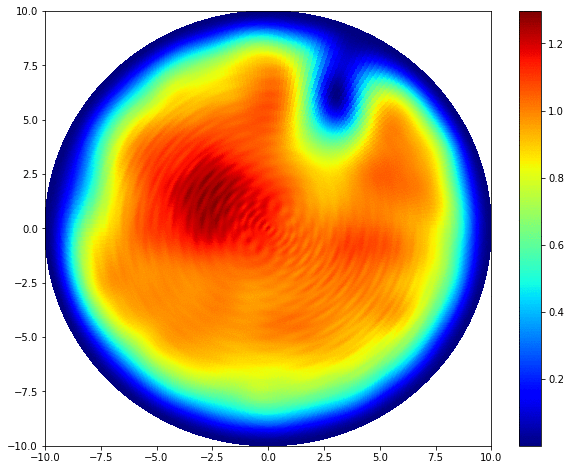
The dynamics of Bose-Einstein condensates (BEC) is completely governed by the time-dependent Gross-Pitaevskii equation:
\[i\hbar \frac{\partial }{\partial t} \psi (r,\theta) = -\frac{\hbar^2}{2m} \nabla^2 \psi + V(r,\theta)\psi + U_0 |\psi|^2 \psi.\]\(\psi (r,\theta)\) is the wave function describing the state of BEC. \(i\) is the imaginary number, \(m\) is the mass of each individual particles, \(\hbar\) is the reduced Planck constant. \(U_0\) represents the interactions between particles, defined as:
\[U_0 = \frac{4 \pi \hbar^2 a_s}{m},\]where \(a_s\) is the boson–boson s-wave scattering length. \(V(r,\theta)\) is the potential. In our case, we want to confine the BECs inside an infinite circular potential well. The potential is then infinite outside the domain, and equals to some constant inside. 2D Bose-Einstein condensates share a lot of common features with classical shallow water systems with surface tension (see Madelung equations), many classical fluid dynamical phenomena, i.e. vortices and gravity waves, can be achieved in BECs.
The key to numerically solve the Gross-Pitaevskii equation is dealing with the Laplacian operator \(\nabla^2\). Due to the infinite potential well, the BEC vanishes at the domain edge (homogeneous Dirichlet boundary condition). This fact makes Fourier-Bessel series an ideal choice to decompse the wave function in the radial direction. We uses the Fast Fourier transform in the azimuthal direcation to isolate all angular modes, followed by a discrete Hankel transform of corresponding order within each mode for radial decomposition. Bessel functions are the eigenfunctions of the Laplacian, and the eigenvalues are their roots. The integration of the Laplacian can be then achieved by a pure spectral time scheme:
\[\nabla^2 \psi (r,\theta) = \sum_{q} \sum_{j} -k_{q,j}^2 a_{q,j} \left[e^{iq \theta}J_q(k_{q,j} r)\right].\]\(a_{q,j}\) is the resulting dicrete Hankel transformed matrix from the original function \(\psi(r,\theta)\), and \(k_{q,j}\) is the \(j\)-th root of Bessel function, \(J_q(k_{q,j}) = 0\).
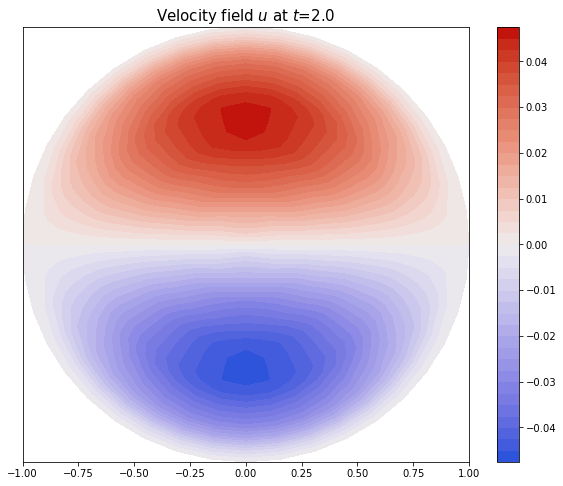
Besides the Gross-Pitaevskii equation, we also apply the solver to study vibration of circular membrane and Poiseuille pipe flows. This project originates from Prof. Nicolas Grisouard’s 2009 Geophysical Fluid Dynamics summer school project at Woods Hole Oceanographic Institution (click here for the original report).