Swirling Kolmogorov Flow
modelling ocean turbulent mixing driven by near-inertial waves :-|
My current master thesis project on ‘Swirling Kolmogorov flow’ is motivated by two aspects, one by the application to oceanography 🌊, the other by the theoretical turbulence research 🤓.
Oceanography 🌊
It is well-known that the internal gravity wave in uniformly stratified fluids forms the ‘St. Andrew’s cross’ pattern as shown in the video above. Inside each beam, shears are generated. However, when geophysical rotation is taken into account, internal waves do not produce a two-dimensional shear flow, but a three-dimensional flow where the direction of the velocity vector changes with depth. This effect is most prominent for near-inertial waves where the dominant restoring force is due to the Coriolis effect (see the figure below for illustration).
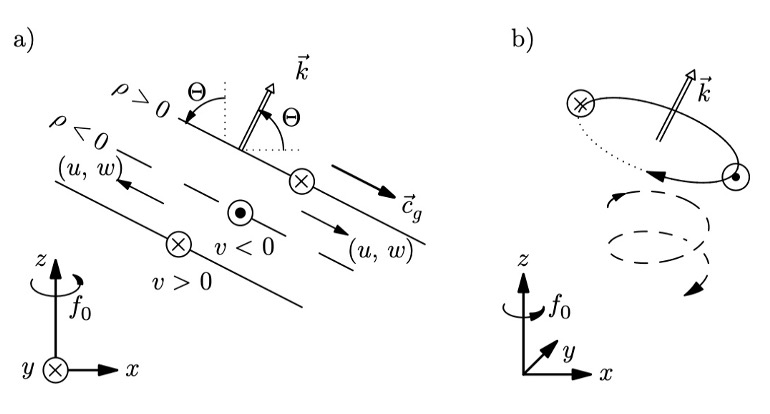
Breaking events of such flow are likely a major contributor to upper-ocean turbulent mixing. Its transports of passive scalars can be a key factor to ocean nutrient distribution.
Turbulence 🌀
A big field of research in fluid mechanics is the Homogeneous Isotropic Turbulence (HIT), proposed by G.I. Taylor himself. Later, the Soviet math lord Andrey Kolmogorov proposed another type of flow on a periodic domain (2D or 3D) driven by a sinusoidal external force in the large scale to study the linear stability in viscous shear flows, which was later named after him as the Kolmogorov flow. Unlike HIT, the Kolmogorov flow is inhomogeneous (mean shear is different everywhere) and anisotropic (direction of the mean flow changes everywhere), the difference between these two types of turbulence (in large-scale, of course, but also in the inertial range) is still an open question.
The swirling🌀 Kolmogorov flow we proposed here is an example of the homogeneous (same shear, hence the energy dissipation, everywhere) yet anisotropic (changing direction) turbulence. Our flow is thus a third type of turbulence, which sits somewhere between the HIT and the regular Kolmogorov flow (hope we can learn more about where it sits towards the end of the project :>). Tons of fun to study!
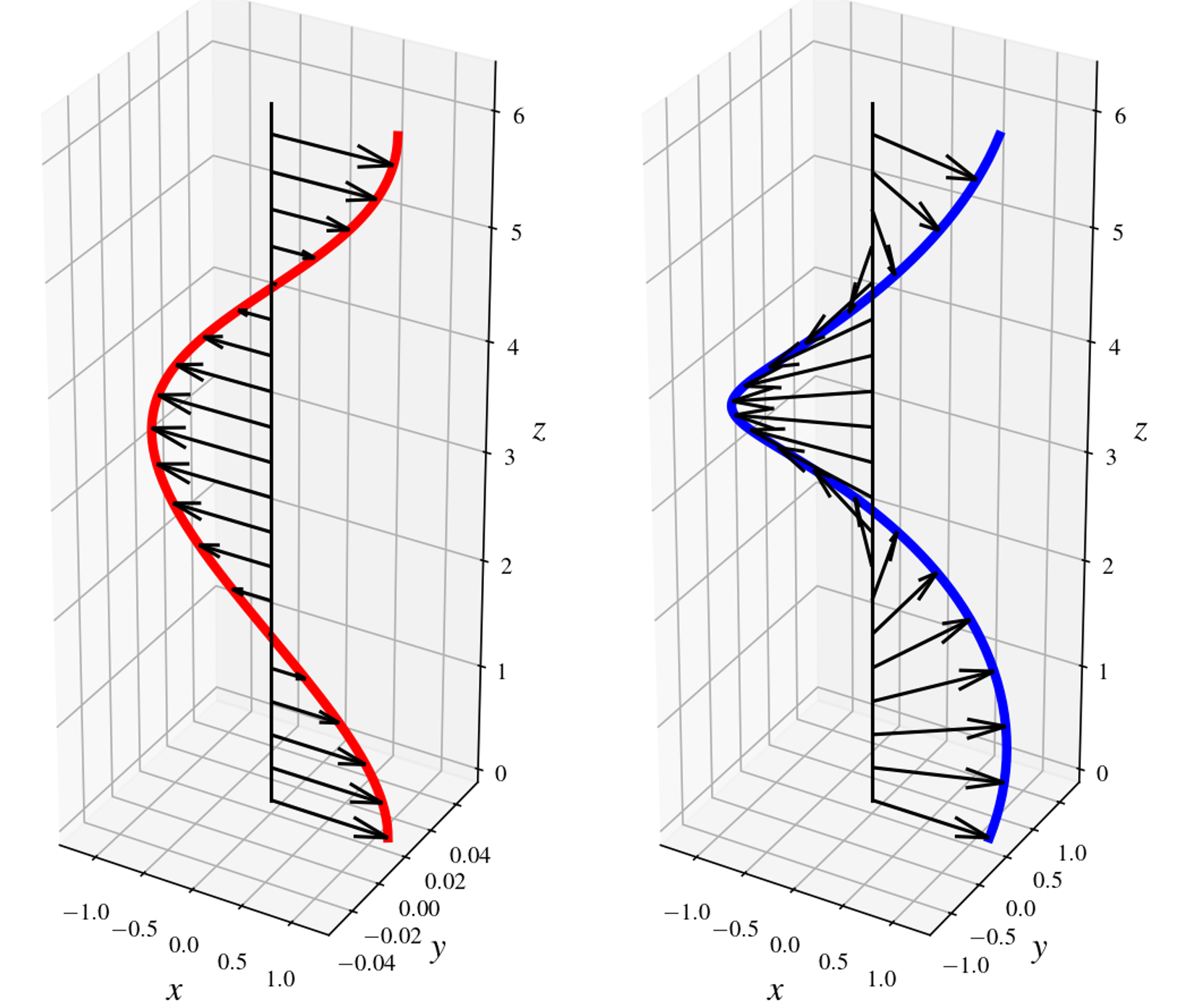
The flow
The swirling Kolmogorov flow is governed by the Navier-Stokes equation for incompressible fluids,
\[\partial_t \mathbf{u} + \mathbf{u}\cdot\nabla\mathbf{u} = -\nabla p + \nu \nabla^2\mathbf{u} + \mathbf{f}\] \[\nabla \cdot \mathbf{u} = 0,\]where the external forcing \(\mathbf{f}\) is given by
\[\mathbf{f} = F_0\left[ \sin(k_f z/L) \hat{e}_x + \cos(k_f z/L) \hat{e}_y\right].\]\(L\) is the forcing scale, which serves as our characteristic length. The trivial steady laminar solution is
\[\mathbf{u}_0(z) = \frac{F_0L^2}{\nu}\big[\sin(k_f z/L) \hat{e}_x + \cos(k_fz/L) \hat{e}_y\big].\]Linear stability analysis
The nondimensional equation for the laminar flow is given by
\[\partial_t \mathbf{u} + \mathbf{u}\cdot\nabla\mathbf{u} = -\nabla p + \frac{1}{\mathrm{Re}}\nabla^2\mathbf{u} + \frac{1}{\mathrm{Re}}\left[ \cos(z)\hat{e}_x + \sin(z)\hat{e}_y \right],\]which we choose the amplitude of the laminar solution as the characteristic velocity \(U_0 = \frac{F_0L^2}{\nu}\). Using the normal mode decomposition and some algebra massage, we obtain the Orr-Sommerfeld equation of the swirling Kolmogorov flow
\[\left(\textcolor{red}{\sigma} + \mathrm{i}\textcolor{green}{\tilde{k}}\tilde{U}\right)\left( \frac{\mathrm{d}^2}{\mathrm{d}z^2} - \textcolor{green}{\tilde{k}} \right)\hat{w} + \mathrm{i}\textcolor{green}{\tilde{k}}\tilde{U}\hat{w} - \frac{1}{\mathrm{Re}}\left( \frac{\mathrm{d}^2}{\mathrm{d}z^2} - \textcolor{green}{\tilde{k}}^2\right)^2\hat{w} = 0,\]where \(\textcolor{red}{\sigma}\) is the growth rate of the unstable mode, \(\textcolor{green}{\tilde{k}}=\sqrt{k^2+l^2}\), \(k\) and \(l\) are the wavenumber of \(x\)- and \(y\)- perturbation, respectively. And \(\tilde{U} = \frac{k\cos(z) + l\sin(z)}{\tilde{k}}\) is the shear flow. Notice the growth rate \(\textcolor{red}{\sigma}\) only depends on the wavenumber magnitude \(\textcolor{green}{\tilde{k}}\), but not on \(k\) or \(l\) independently.
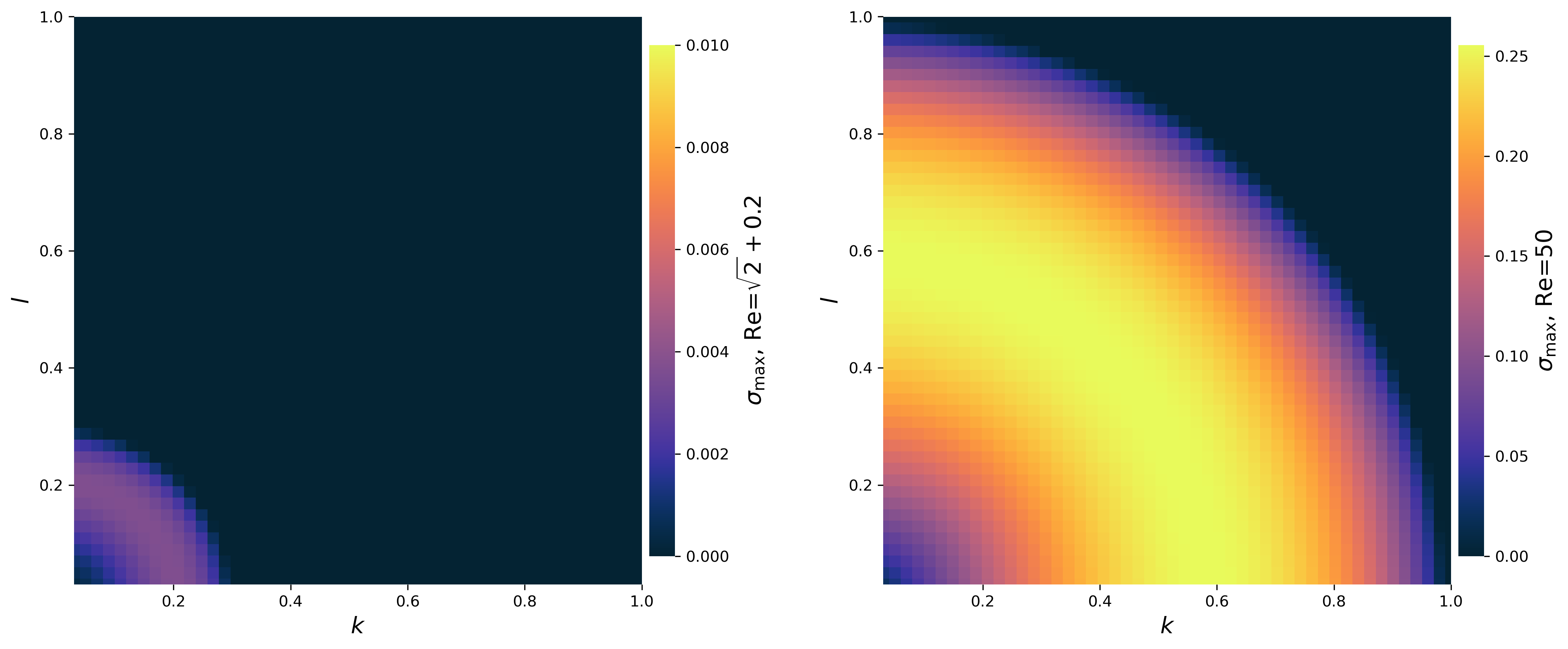
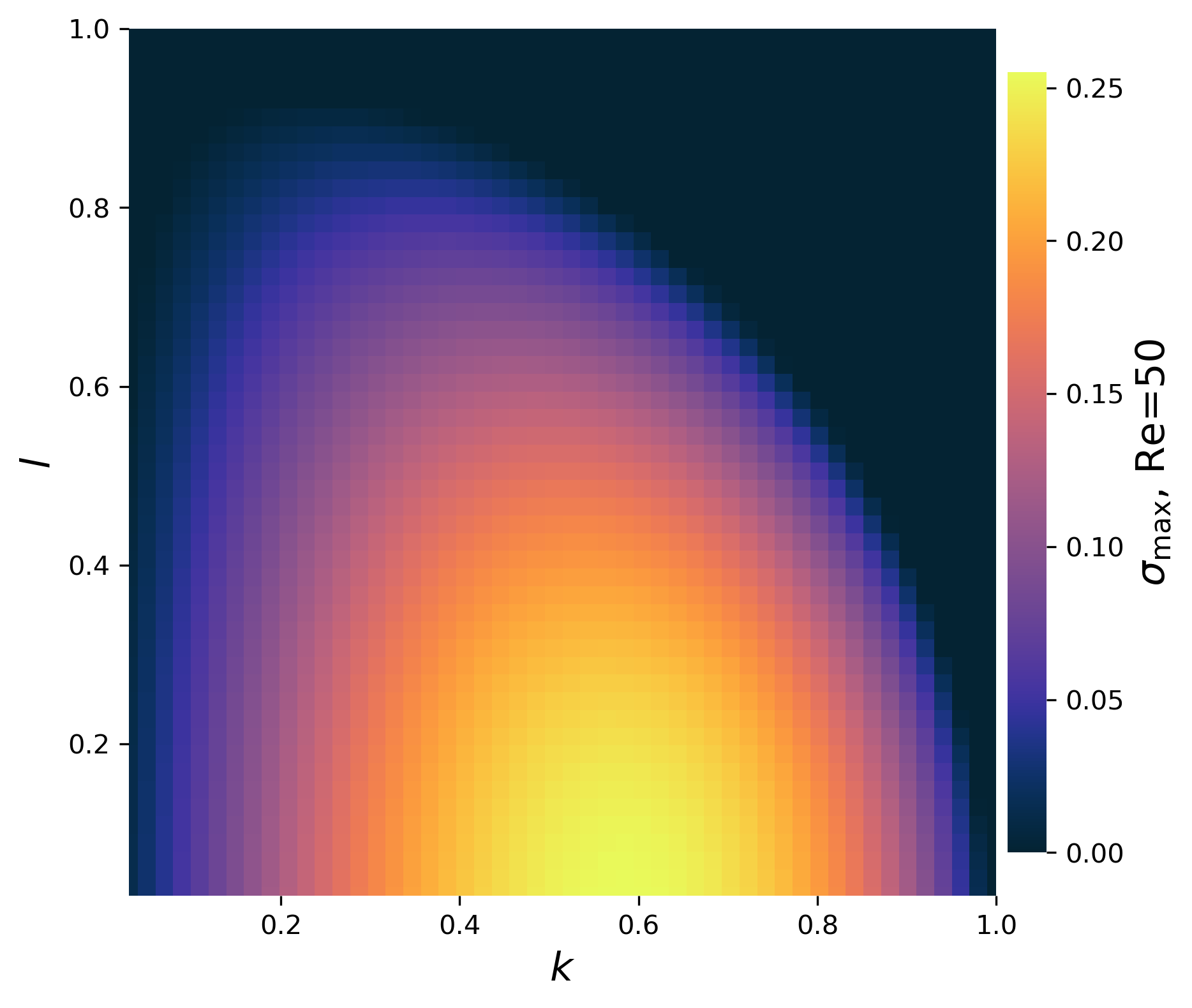
First notice the swirling Kolmogorov flow does not alter the critical Reynolds number \(\mathrm{Re}_c = \sqrt{2}\) where the laminar solution becomes unstable. This is a famous result given by Kolmogorov’s students Meshalkin, L. D., & Sinai, I. G. (1961).
Also notice the cute donut shape of the swirling’s heat map. The swirling flow is sensitive to perturbation in both \(x\)- and \(y\)-directions, as predicted by the Orr-Sommerfeld equation. As reference, the right-most figure is the heat map of a regular Kolmogorov flow, where the flow is only sensitive to perturbation in \(x\)-direction and suppressed by presence of \(y\)-perturbation.
Some simulation results
To understand the transports of passive scalar, and also to better visualize the flow, we add a passive scalar fluctuation \(\theta\), governed by
\[\partial_t \theta + \mathbf{u}\cdot\nabla\theta = \kappa \nabla^2\theta - \mathbf{u}\cdot\nabla\langle\Theta\rangle,\]where \(\kappa\) is the scalar dissipation rate, we chose the Schmidt number \(\mathrm{Sc} = \frac{\nu}{\kappa}=1\). The fluctuation \(\theta\) is sustained by a background vertical mean scalar gradient \(\nabla\langle\Theta\rangle=\hat{e}_z\).
Yeah I know there was a lot of annoying math… Now just sit back and enjoy some beautiful turbulence movies! 😇🤤 All the following videos are showing the 2D \(x\)-\(z\) plane slice at \(y=\pi\).
So, what’s going on with this large-scale vertical motion when we increase the aspect ratio \(\Gamma\)? Is it physical? Or it is just some artifact due to the periodic boundary condition? To further investigate this, we performed simulations on a 3 by 3 by 3 domain, i.e. \(L_x=L_y= L_z=6\pi\), while keeping the forcing scale the same, so there are three whole wavelengths along the vertical axis. Here come some more beautiful movies! 🎆
Our hypothesis is that the large-scale motion as well as the vortex pair in the single Kolmogorov flow is due to the inverse cascade. Since the injecting force as well as the mean flow is essentially 2D. These are gone in the swirling case!
More to come! 🤩
-
Increase Reynolds number, numerical simulations at higher resolution.
- Investigate the impact of Reynolds numbers on swirling flow.
- Better resolved inertial range – anisotropy effects?
- Friction factor (mean flow vs dissipation).
- Effect on mixing statistics.
-
Domain size effects
- Inverse cascade in Kolmogorov flow? (2D condensate). Need some math here…
- What about the swirling case?
- Can we reach a box-independent state?
- Large-scale dynamics?