Discrete Dini transform

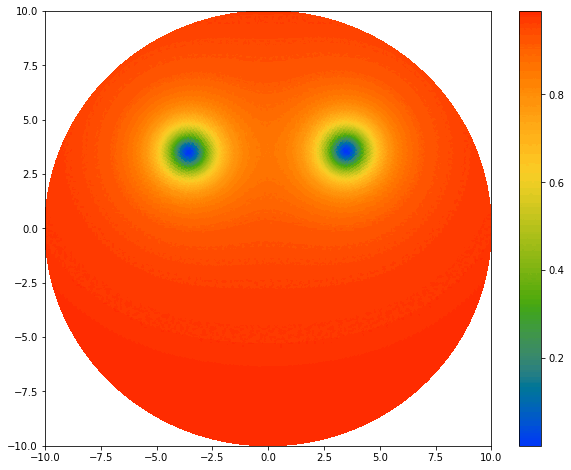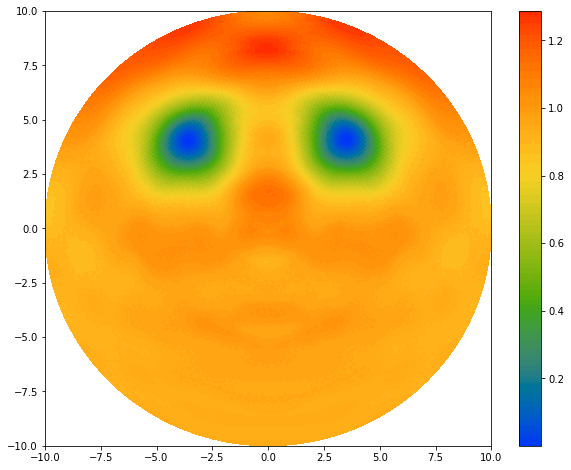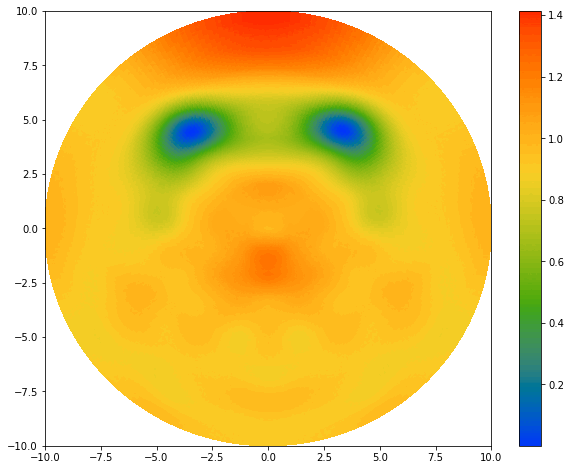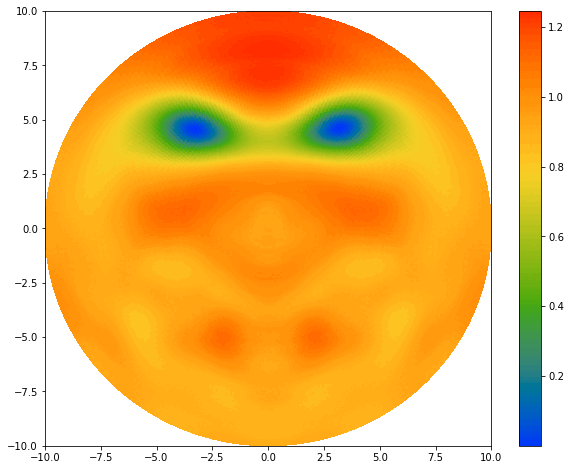
The origin of this ‘Discrete Dini transform’ project emerges from the spectral laplacian solver. If you look closely at the BEC plots here, you will realize they are missing the boundary layer comparing to the plots of laplacian solver project. What’s happening here?

In the previous case, the wave function \(\psi(r,\theta)\) is subjected to the homogeneous Dirichlet boundary condition due to the infinite potential well, where \(\psi = 0\) at the edge. Here, instead of itself vanishing, only the wave function’s radial derivative vanishes at the boundary (Don’t ask why this is the case, I just want it to be :>):

This situation is called the homogeneous Neumann boundary condition. To solve the Laplacian operator under such boundary condition, we need a new type of discrete transform method. We currently named it the ‘Discrete Dini transform’ because we are using Dini series to decompose the raidal functions. Dini series can be intuitively regarded as a variation of Fourier-Bessel sereis, because instead of using zeros of Bessel function, it uses the maxima \(J'_q(\lambda_{q,k})=0\) to ensure the right boundary condition (this is the special case for Neumann condition, the more general forms are in the project’s profile picture). But it is mathematically different from the Fourier-Bessel seris with a lot more nuance.

Currently, simulation codes were written and working successfully (with some undesired artifacts). However, the math behind it still remains unclear. I am working with Prof. Natalie Baddour trying to establish this method rigorously. The ultimate goal of this project is to solve the Laplacian under arbitrary boundary conditions.